| The Manifesto | | | The 8 Houses | | | Texts and Articles | | | Review | | | Links | | | ACCUEIL (FR) | | | HOME (EN) |
| A Mathematical Formulation of Harmograms and the Strength of Number in Astral Charts
by Miguel García Ferrández |
Abstract
Starting with a historical perspective, the mathematical equivalent of Harmogram computation, in terms of the Fourier Spectrum of some special functions, is presented. The Fourier Analysis is used to formalize one astrological technique inside of John Addey's Harmonic Theory, and one outside. The mathematical tools presented are applied to discuss some obscure or imprecise points in harmonic research and practice, specifically to the role of conjunctions in harmonic aspect sets, and to the problem of aspects orb. A conducting thread through the paper is the author's awareness of the fruitfulness of Fourier Theory as a paradigm from which to model Astrology. Appendix One gives mathematical details of the special functions used. Appendix Two -almost an afterthought- gives the harmogram formulation of the Cyclic Index.
Introduction. Harmograms in Perspective
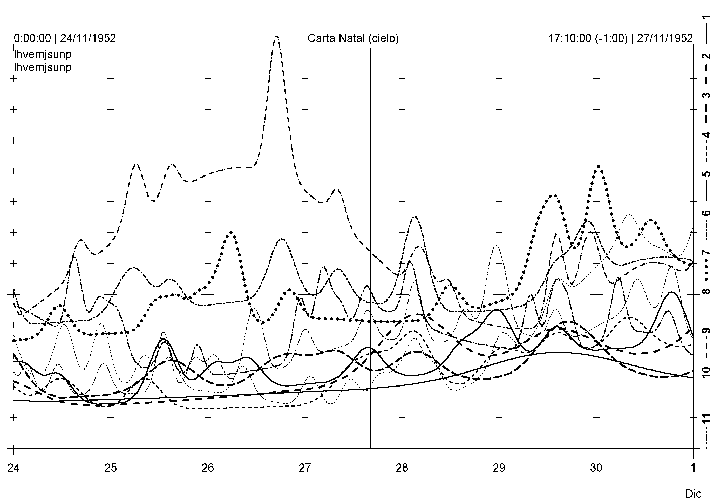
A Harmogram (Kollerstrom & O'Neill, 1991) is a graph of the evolution with time of the strength of numbers as computed from the harmonic aspects (derived from the integer divisions of the circle in equal parts, harmonic does not mean 'harmonious') between the planetary positions in the sky. Central to it (and usually central in it) is a mark at the moment of birth of some entity, which is the subject of the harmogram. Being a computer programmer and researcher on harmonics myself, I built several years ago a module to compute and draw harmograms (though at the time I didn't knew of this name), a sample of which is depicted in figure 1.
Figure 1.- Harmogram in the neighborhood of a birth

In figure 1 it can be seen the evolution of the strength of the eleven first natural numbers in the neighborhood of a birth, and the insertion point of the birth itself. Each line in that figure is the trace of one harmonic number. A colleague (T. Maciá) and I are currently experimenting with this tool as a means to assign people (both famous and ordinary) to dominating number, with some success.
I arrived at my earlier version of the harmogram starting from the idea of harmonic transits (Maciá & García, Peñíscola 1994). Approaching the birth date -to investigate the harmonic neighborhood of a chart-, all harmonics peak as the transiting planets get near the natal positions. So I suppressed the transiting aspects to the birth chart and considered only the aspects in the sky. I.e., rediscovered the harmogram.
In any case, I don't claim anything concerning originality. I can trace back the idea of depicting some measure of the intensity of planetary aspects as a function of time to Lambert Brahy's La Clef des Evenements Mondiaux. And the idea of harmonic aspects can be traced back to Kepler. Also, the work of Gouchon and Barbault with the cyclic index can easily be proved to be the use of the [reversed] harmonic one of the harmogram of Jupiter to Pluto, with an intensity function -see what follows- of very simple facture (Appendix Two, also García, 1991).
But, even having the tool ready, I did not get interested in harmograms, as a means to classify people to investigate the essence of harmonic numbers, until I read Kollerstrom & O'Neill's book. So, some of the research done lately by T. Maciá and I, using that tool (Barcelona, 1997), is in debt to their thought provoking work.
Harmonics
My interest in harmonics began when -and arose quickly after- I read John Addey's seminal work (Harmonics in Astrology, 1976). Not much later I had access to the excellent book by David Hamblin (Harmonic Charts, 1983) that makes a practical tool out of harmonic theory. Hamblin also makes a very lucid exposition of the light and dark spots of the theory. To my present discourse, the interesting concept is that of a strong harmonic chart, used by Hamblin to select case examples for his book.
I embrace wholly -from a technical point of view as defined in Dean (1996), not from a metaphysical one- Addey's idea that (almost) all of Astrology's can be explained as the manifestation of numerical principles in the sublunary world (Maciá & García, Barcelona 1997). So, I adhere to Addey´s implicit programma, which is -as I perceive it- that investigating the intrinsic nature of numbers should be among the main objectives of astrological research.
Both techniques, harmograms and strong harmonic charts, are useful tools to investigate the harmonic nature of the astrological phenomena. And both are intended to highlight the numbers that are strong in a chart. But both, as practical tools, have weak points. Harmograms are dependent of the intensity function used to compute the number strength (through several years I have made near a thousand of trials, with different charts and functions, to prove it to myself). The trained eye of the experienced astrologer (as Hamblin undoubtedly has it) is a scarce an elusive asset. A mathematical model of [preferably] both would be a welcome contribution. I think that I can make it. But first, introducing some concepts is in order.
Astrodynes: Functions of Intensity in the Circle
The dyne is an unit of force in Physics. The force is what causes the movement, of there the root 'dyn' in 'dynamics' or 'dynamo'. 'Astrodynes' could be translated for 'the force of the stars [to produce movement]'. In this paper it is essential to understand the concept of function of intensity of aspects; what we could call aspect astrodynes, aspectodynes or harmodynes.
In the analysis of the harmograms, and in that of the C60, it is necessary to have a clear idea of what we mean for 'function of intensity of aspects': a function that associates a value of force, some astrodynes, to each point of the circle that represents the angular separation between two planets or points of the chart. Almost always, one of these functions it is a function that is zero in most of the circle; only in the vicinities of an aspect, in the habitual sense, it is different from zero. I'll present enough examples in the text.
Harmonic Vector of a Collection of Points in the Circle
Around the spring of 1989, I had an idea visualizing the planets of a chart making 'plink', somewhere in their diurnal cycle. "A 'plink' somewhere in a circle" is the common language version of the mathematical function 'Periodic Delta of Dirac'. So I started to play with the notion, switching to the zodiacal circle and soon arriving to the formulation of the Harmonic Vector (HV): The Fourier spectrum of the sum of one Delta of Dirac for each planet in the chart (see Appendix One). Later, a friend informed me that A. Boudineau had proposed a simpler version named Planetary Resultant (Boudineau, 1985). In fact the first term, not counting harmonic zero, of my harmonic vector.
Each harmonic number h has a pair of values in the HV, an amplitude A(h) and a phase W(h). A pair that I call the h-th coordinate of the harmonic vector; a notation that is in agreement with functional spaces theory (Rudin, 1987). As from the Theory of Hilbert Spaces, coordinate 0 needs a special treatment, dependent of the orthonormality of the sine/cosine base functions. I have chosen a convenient factor in order to get a simple form for Parseval's formula -see below-.
My work, of a bit less than two years with the harmonic vector, was presented in a Spanish Astrology Congress (García, 1991). Figure 2 shows the computer version of the harmonic vector of a chart, designed (not very successfully) to prompt its users to investigate the device. Other uses of the Harmonic Vector appeared in García (Madrid, 1994) and in Maciá & García (Valencia, 1994).
Figure 2.- Harmonic Vector of a chart

In the following discussion, some confusion might arise from the fact that we are mingling harmonic numbers, generators of harmonic charts, with the harmonics -the terms- of the Fourier spectrum. Some times the harmonic terms in the Fourier spectrum will be the subharmonics of the harmonic number of a [harmonic] chart -do you see what I mean?-. I've tried to make the distinction in the text as clear as possible. The terms in a Fourier spectrum can also be called the Fourier Coefficients.
The Set of Parts from Zero Aries
If we have a collection of points (read: planets) in the Zodiac, we can build the Set of Parts from Zero Aries by combining each planet with any other in the collection (and with itself), adding to the set their angular separation measured from 0º Aries. In fact, all the points deriving from the formula:
0º Aries + Planet1 - Planet2 as Planet1 and Planet2 visit all the planets in the collection.
From n points in the collection we get n2 parts in the set. Akin to Arabic Parts, but using the Vernal Point instead of the Ascendant of the chart. Of course, we'll get n 'extra' parts of type: this-planet-with-itself at zero Aries. Contrary to common sense Astrology, but essential for the mathematical treatment.
The notable fact about this construction is that its Fourier spectrum of Deltas of Dirac at each Part (the Harmonic Vector of the Set, regarded as an independent collection of points) derives from the HV of the original collection by means of a simple formula. I'll omit the mathematics of the proof.
Let {[A(k), W(k)], k=0 to infinity} be the HV of the original collection. As stated, A(k) is the amplitude of the k-th harmonic, and W(k) is its phase. For k=0, the pair [A(0),W(0)] of a collection of n points, named some times harmonic zero, is always [n,0]. Amplitude equal to n, and phase zero.
The set of Parts from 0º Aries of the collection has PA = {[A2(k),0]} as harmonic vector. Amplitude squared, and phase zero. Again, for k=0, we get [n2,0] as harmonic zero. This property, that of being the terms of the HV of one collection the square of the terms of the other, does not hold if we don't count each planet with itself in the set of Parts.
Instantaneous Strength of Number in a Harmogram as Parseval's Formula for the Inner Product Integral of two Functions
Nearing our main theme, let us consider the computation of the instantaneous value of a harmonic trace in the harmogram, i.e. the strength of that particular harmonic number of the chart of a moment in time. We add the intensity of the aspects, with base the harmonic number, cast from a planet over any other (distinct) in the chart. We may, as Kollerstrom & O'Neill do, suppress the conjunction from the account; or include it in the tally, as T. Maciá and I have proposed (Peñíscola 1994, Barcelona 1997) and are currently doing in our research. A point that I'm going to discuss later.
The intensity of a harmonic aspect set, varying as a function of the angular distance from a planet to another, is what I call Harmogram Intensity Function. Of course, as a planet moves from the conjunction along the circle of angular separation, it goes in and out of aspect orb with the other as he passes the aspects in the set. And one expects that the intensity will become zero away from the partile aspects.
Let's try an alternate definition: a set of harmonic aspects is the set of zones in the circle of angular separation of two points, in which the value of the intensity function is not negligible. Or also, depending on context, it can be considered the set of angular measures of the centers of the peaks (the maxima) of the intensity function. I propose to the reader, as exercise before going on reading, to try to discover why that simplistic definition does not work, in practice, to investigate the strength of numbers in a chart. That it does not work was the motivation for this paper. So let's forget this definition and get back to the intensity functions. The second way of defining the term 'set of harmonic aspects' will reappear with a more valid purpose.
Figure 3 depicts the function proposed -and used- by Kollerstrom & O'Neill (K&O), and the one used by T. Maciá and I (M&G), both for harmonic five as example. Plus a third function of the type used by me, with a different orb, that I'll discuss later. The figure is compressed to show detail, and off-center by 180 degrees (zodiacally speaking) to highlight the symmetry of this kind of functions.
Figure 3.- Three Harmogram intensity functions

Whatever be the case, we are using the planets in the collection to scan a function of intensity centered at each planet of the chart, as if a field of force where emanating from that planet. And we add the contribution of each planet into a total which is the instantaneous value of the harmogram for that chart.
The convenient outcome is that, in so doing, we are in fact computing the inner product integral <PA,f > between the intensity of aspects function f and the sum of Deltas of Dirac over the Set of Parts, already defined, PA. Working in the space of Fourier spectra, this inner product integral becomes a simple series -as supported by Parseval's Theorem (Apostol; also Carslaw, 1930)-, that, if the intensity function f is more or less well behaved, collapses to a simpler sum of a few terms.
Let {[A(k),W(k)]} be as defined earlier, and let {[F(k),O(k)]} be the Fourier spectrum of the function of intensity of aspects. If this last function has symmetry with respect to the planet generating it, O(k)=0º or 180º for every k. In which case the inner product integral becomes:
S A2(k) x F(k),
this infinite sum will be, in practice, over all the terms for which F(k) is not almost zero. For this formula to work properly, we have to apply a rule of signs that gives a negative value to F(k) when O(k)=180. I will call this formula Parseval's Formula for obvious reasons.
Mathematical note: The sums of Deltas of Dirac that I'm using are themselves distributions rather than functions (Zemanian, 1965), what does not invalidate Parseval's Formula.
Note on implementation: To get, in a computer program, an exact correspondence between the value computed by a K&O Harmogram style code and a Parseval's Formula style code is essential to add all the terms of the Fourier series that are big enough, especially term zero. I had to recheck several times the mathematical derivation of this result, and the computer program I concocted to test it, before I got a true correspondence. As the Harmogram device does not tally each planet with itself, you should subtract n points from the Parseval value, for an n-planet set, and divide the result by two, to get identical results. End of Notes.
Figure 4.- Fourier Spectra of the functions in figure 3

Figure 4 shows the Fourier spectrum of the functions in figure 3. The three functions are 'normalized' to a peak value of one (L(infinity) norm, not the more common L2 or L1 norms). All intensity functions, used in this paper to draw harmograms, will be so normalized. To the left of each spectrum is the peaky figure of intensity in the circle. The spectra are not drawn to the same scale to gain detail, and the values of the amplitudes in the graph are multiplied by 10000. The descending lines in the first spectrum are the harmonics not multiples of five, needed to suppress the peak at the conjunction. All three spectra quickly vanish to zero, as can be proved. Our function, being almost a gaussian, behaves even better than the one used by K&O.
It is worth noting (Fig. 4) that the exclusion of conjunctions in the intensity function distorts, so speaking, the spectrum. You can only use the same intensity function for subharmonics -an implicit demand in Addey´s theory- if that intensity function has star symmetry. Being the case, the spectrum of a symmetric s-point star, with orb W/s, contains exactly the terms of the spectrum of a single peak at zero degrees, with orb W, -the spectrum for a conjunction aspect- spread over the harmonics that are multiples of s. See Figure 5. A result that I'll use later in 'An Alternate Procedure for Computing Harmograms'. Note that the lower spectrum is drawn with trice as many harmonic terms than the uppermost. And note also the resulting zero amplitude of the harmonic terms not multiples of three (not labeled in the figure).
Figure 5.- FS of a three points star vs. a 'one point star'

In the three figures, 3, 4 and 5, orbs are 'equated' to harmonic one, as proposed by Addey. That is to say that the true orb of the aspects is the annotated orb divided by the harmonic number. A rule of thumb that begins to have a mathematical foundation.
The Effect of Varying Orb and a Further Discussion of The Missing Peak
Figure 4 shows the spectra, for the same harmonic number, of two gaussian-like intensity functions of different orb. As can be seen, the effect of decreasing the orb amounts to decreasing the rate of damping of the terms in the spectrum. In fact, the profile of the Fourier spectrum of a gaussian function is another gaussian, and the product of the rate of decay -loosely speaking- of both functions is a constant value. So, varying the orb is akin to modifying the number of subharmonics that are accounted for in Parseval's formula. The narrower the orb, the higher the subharmonics included.
Another important fact to be learned from figure 4 is that a missing peak in the intensity function, at the conjunction, complicates instead of simplifying the spectrum. I have commented the matter above. There is a different line of discourse to justify the inclusion of the conjunction in the intensity function, as we do here in Spain. And it is that the ever repeated statement, in the literature on harmonics, that (I quote Hawley, 1995) As the 0º position is common to all harmonic aspects, its contribution can be omitted when determining ... (see also Kollerstrom & O'Neill 1991, p1) completely misses the point in harmonic theory.
The point is that the set of natural numbers has a lattice (net-like) structure with the partial ordering m divides n, that replicates in (is isomorphic to) the sublattice of all the multiples of a number, for every natural number. In other words, the opposition is present in all even harmonics, the trine is present in all numbers multiple of three, etc. Lets call harmonic aspects set of a number to the set of all angular measures that are multiples of that's integer fraction of the circle. The aspect set of number nine includes the whole set of aspects of number three, not only the conjunction. The aspect set of number ten includes the five aspects of number five, and the opposition. Etc.
So, either you start pruning aspects from all decomposable harmonic numbers -those like 4, 6, 8, 9, etc. that are not prime-, or you include even the conjunction in the intensity function. Also, we should never forget that Nature likes symmetry. As a matter of fact, after experimenting for a relatively short time with pruned harmonic aspect sets -even coining a term, that of proper aspects of a harmonic number, (Maciá & García, Barcelona 1997)-, we have reverted to using the whole sets.
Note: As I read The Eureka Effect (K&O, 1996), after having almost completed this paper, I understood the sensible reasons adduced by the authors for not including the conjunction in the aspect totals. But I am convinced that the true nature of astrological phenomena is a bit different from the way it is generally perceived these days -as I gather by reading the available literature-. And I hope that I'm casting some light upon the subject with this paper.
Measuring the Strength of Number [One] in a Chart
Hamblin did a thorough and convincing job in his book to expose the possibilities of harmonic charts, both as aides to natal astrology and as research tools. But, as I pointed earlier, his expertise and insight cannot be purchased on the lab supplies store next street.
As I discovered the relationship between Fourier spectra and harmogram intensity of harmonics, I realized that I had the tool to attempt to quantify Hamblin's criteria. Before I present the data, it is convenient to review his procedure.
Hamblin defines the strength of a chart, be it harmonic or otherwise, as dependent of the closeness and interconnection of aspects and aspect patterns. Though it is possible, with hindsight, to deduce from theory the Fourier Analysis equivalent of that definition, I choose to go the empirical way, that I go on exposing: As he presents example after example of relevant charts, for every studied harmonic number, we are entitled to suppose that he values each chart irrespective of the harmonic number. It is worth noting that, on closer scrutiny, that is not exactly the case with his examples (no criticism intended), but for the sake of fairness and simplicity, let us assume so.
One point in which the harmonic number visibly intervenes is in the maximum separation between Mercury, Venus and the Sun. There are other astronomical phenomena, dependent of the harmonic number, that influence the spread of the planets in a harmonic chart, as has been rightly pointed out by other authors (Hawley, 1995). So I won't prosecute the issue.
As the harmonic number is not considered to judge the strength of a harmonic chart, we can infer that he is measuring the strength of number one in that chart. Of course, number one in a harmonic chart is that harmonic's number in the radix.
The Procedure
We have the Harmogram, with a repertoire of intensity functions and orbs, to measure the strength of a number in a chart, and have the Fourier Analysis equivalent of that device. So let's do reverse engineering on the output of Mr. Hamblin. To try every possible harmogram function with Hamblin's charts would be an impossible task. Fortunately Fourier Analysis can unveil it for us.
For each chart in Hamblin's sample we compute the Fourier spectrum of the Deltas of Dirac (my Harmonic Vector) of the appropriate harmonic chart. And tally the squares of the amplitudes of the Fourier coefficients in a table, graphically depicted in figure 6 and drawn as if it were a Fourier spectrum. In that table we are adding heterogeneous harmonics in each entry, but I'm confident in that the preceding discussion validates the procedure. We are contemplating each chart as if it were harmonic one, a radix.
Figure 6.- Hamblins charts analyzed
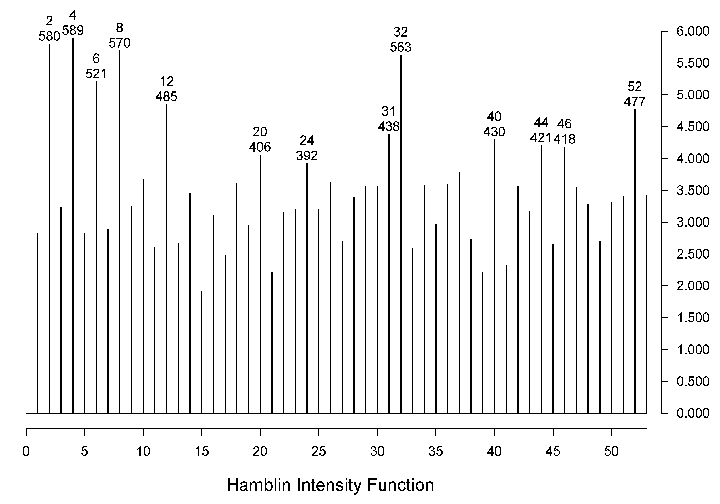
After having completed the totals, the resulting graph of values should be an estimate of the Fourier spectrum of the [searched for] Intensity Function of the Harmogram, implicit in Hamblin's work.
The Data
Working with a set composed of 4 harmonic-four charts, 9 harmonics-five and seven, and 10 harmonic-nine, for a total of 32 charts. And adding the squared amplitudes of the Harmonic Vector corresponding to each harmonic chart, figure 6 reveals the weighty subharmonics for judging the strength of a chart. Only one of the charts in the first part of the book was omitted due to being, in Hamblins words, a weaker one. Plus a couple, or so, whose birth data were not available.
It is relieving to find at least four of the first five powers of two as prominent subharmonics in the sample. Also numbers six and twelve appear as lesser but noticeable harmonics, not so three -perhaps too easygoing a number to give strength to a chart- In any case it's an astrologer's criterion. It's intriguing the low value of harmonic sixteen. The sample of charts is not very large. Also, I don't find relevant a statistical analysis of significance. Years of analyzing reams of samples of natal data have convinced me that only replication can validate a statistical inference.
Table 1 summarizes the prominent harmonics. To get up to ten prominent harmonics -to compare table 1 with table 2 later- you have to include rare or high harmonics that could be artifacts of the smallness of the sample.
Table 1. Harmonic weights by Hamblin
Harmonic 4 2 8 32 6 12 52 31 40 44 Amplitude 5.89 5.80 5.70 5.63 5.21 4.85 4.77 4.38 4.30 4.21 The Inferred Intensity Function. An Alternate Procedure for Computing Harmograms
To sum up this result, one is tempted to build a function from the prominent harmonics obtained. And I've done so in figure 7 with the first six values in table 1. But the suggestion is to omit the graph; to work instead with the harmonic vectors of the charts; and to weight them with the coefficients in figure 6. Or use some other set of weights that this or that theory may propose.
Figure 7.- Synthesis of a Harmogram function from Hamblins data

If we have so chosen a set of weights for subharmonics {F(k)}, i.e. use a star symmetric intensity function: to judge the strength of number h in a chart, we can proceed as follows:
I. - Compute the coordinates in the Harmonic Vector for h, 2h, 3h, ... (k x h), etc.;
II. - Take their squares and multiply by the weights (forming terms like A2(k x h) x F(k)); and
III. - Add the products to get a weighted total: S A2(k x h) x F(k) adding for k=0,1,2,...
IV. - (optional) subtract from the total the number of the planets included and divide by two.
If we prefer to omit the conjunction (or use any other intensity function without h-star symmetry) we have to extend the sum to all the coordinates of the HV for which the Fourier coefficient of the intensity function is not (almost) zero. You have to tailor a specific intensity function, for each harmonic number h; compute the Fourier coefficients {Fh(k)} for that function; and compute: S A2(k) x Fh(k).
Note: Don't jump to too many conclusions looking at Figure 7. I hope that, including the analysis of Hamblins data in this paper, I'm showing the complexity of harmonic phenomena as qualitatively perceived by astrologers. I do not intend to propose an alternate -or weird- function shape for harmograms. I'm just trying to share insight into the main theme.
One Example Outside of Addey's School
Here in Spain is well known the work of our dean in astrological research, Demetrio Santos. His C-60 device defines a value of Astrodynes, computed over the Zodiac from the planetary aspects to each degree, plus a means of directing the Ascendant, in order to predict crises in the native's life.
In graphical form we get a chronological dial with an intensity of 'would be' crises, as is depicted in figure 8. Mario Balagué, in a private work session, proposed the pictorial representation to me in 1993, and I included it in my computer program. Since then, a lot of researchers and consulting astrologers are using the graphs here. And are also extending the technique, by changing the arc of direction of D. Santos, to other cycles and uses.
Figure 8.- Santos C-60 astrodyne dial

The pertaining fact about the astrodyne function of D. Santos is that it is computed by adding the contribution of each planet. Each planet 'generates' a function of astrodyne intensity, as is the case with harmograms. The symmetry of the graph of intensity for a single planet will give a zero-phase Fourier spectrum -with some negative amplitudes, see bellow-. Though, now, this symmetry is not a required property for the analysis.
Here I include the Fourier treatment of this device because, while diverging greatly in origin and purpose, it gives a result similar enough to the examples of Hamblin. One set of weights -Fourier coefficients- comes from the analyzed practice of an astrologer, the other from an intensity function that sprouts straight out of pure -and at times questionable- theory, however successful in practice.
For the sake of clarity I should point out that this astrodyne function was not intended to compute harmograms. Also, a scanning of the intensity function of each planet is not performed by the other planets. So, it is not fully legitimate to speak of 'harmonic weights'. Or could, in any case, be misleading after having discussed here Hamblins data. Instead, let us view a harmogram intensity function as a mix of harmonic 'energies' and then compare it with another mix: Santos astrodyne function.
Figure 9a.- Santos C-60 one planet intensity function shape

Be it, in figure 9a, the intensity function of the astrodynes cast by a planet at 0º Aries, as proposed by Santos and Balagué. And be it, in figure 9b, its Fourier spectrum. Table 2 lists the first ten more prominent harmonics in decreasing order of magnitude.
Figure 9b.- Santos C-60 one planet intensity function spectrum

Table 2. Harmonic weights by D. Santos
Harmonic 12 8 24 16 4 6 20 18 10 36 Amplitude 1.360 1.023 0.960 0.815 0.726 0.615 0.544 0.388 0.384 0.287 The graph and table 2 speak for themselves. Again we find the even harmonic numbers as prominent. Again, a lack of prominence of some of the small valued integers, numbers one, two, three and five, etc. Etc. As the function is partly based on a four spokes wheel, we have the first multiples of 4 among the prominent harmonics. Id. id. id. for number 12 series.
The 180 phased harmonics -the descending lines in figure 9b-, equivalent to negative weights, are in any case of small value. They arise out of a certain peakyness of the intensity function, combined with a slight tendency in the function to favor subharmonic oppositions.
Note: Santos (1976) does not define a value and/or shape for the width (the orb) of each aspect, only a value of the intensity of the peak for each aspect. At least until very recently, within the work presenting a zodiacal modulator that he names 'chromatism' (Santos, 1994), in which he explicitly defines shape and orb for each aspect. The amplitude for the peaks was set roughly to six degrees by M. Balagué in an early implementation of the C-60 dial, that later, by my concourse, became the tool in general use here. Of course, the width of the peak reflects in the Fourier spectrum. I've chosen the regular implementation as example to analyze.
Conclusions
Apart from contributing with a mathematical model for harmograms, an always-convenient resource -whatever its equations- in any discipline that aspires to a scientific approach to the pertaining phenomena, this paper shows, in the particulars of the mathematical model, that harmograms in fact measure the projection of the planetary 'energies' onto each natural number.
If we accept one of the harmonic hypotheses implicit in Addey's work, the one that says that every natural number manifests in all its multiples (Addey, 1972, 1976); and we consider that the energy of a pure sine wave is proportional to the square of its amplitude; then we arrive to a model for harmograms that is also a quasi-physical model.
Accepting that line of discourse, the harmogram rises, from the level of a serendipitous artifact, to the category of (quasi-) scientific instrument. This author (me) has become convinced, in the last four years -including in those years the use of my first draft for the tool: harmonic transits (Maciá & García, Peñíscola 1994)-, that the harmogram is a very effective tool. Indeed, I got interested in a mathematical model of it because of that effectiveness. Perhaps the reborn Astrology, as heralded by Addey (1972), is coming of age.
As for the analysis of Hamblin and Santos harmonic mixes, there is no definite conclusion. The spectra obtained from both sets of data differ qualitatively from a typical harmogram function. The emphasis on both is on harmonics that are multiples of two, even on the powers of two.
Should we change the shape of the intensity functions that we use to compute the intensity of harmonic numbers in harmograms? I'm not really sure. Parsimony counsels, for intensity peaks and/or for Fourier spectra, wave shapes of the type already in use (gaussian or gaussian-like); as functions of this type are usually encountered in other branches of the natural Sciences.
Should we, using the current harmogram devices, look for the strength of number h of a moment of time in the harmogram trace of number 2h, as the even harmonics are the more prominent in the studied samples/waves? In the trace of 4h? Again I'm not sure, but inclined to answer NO. I think that, before we make choices, we need a better understanding of the underlying phenomena.
What ever be the case, what should be clear is that the strength of numbers as measured by harmograms differs from the criteria of the experienced astrologer. It should not be surprising that astrologers give more weight to even harmonics, as two is the first number of manifestation (see Addey, Hamblin, etc.). I do support the theory that the weights used by astrologers in all kinds of 'quantitative' Astrology depend upon the intended purpose of the measuring device in which they are used. It's an open issue, well outside the scope of this paper.
There is another way to face the issue of the relative weight of harmonics (or of the intensity function spectra), considering all harmonics simultaneously in a circle, along the lines initiated on Maciá & García (Barcelona 1997); that, again, is beyond the scope of this paper.
Acknowledgments
As can be inferred from the text and the references, my work in harmonics, including the theory and use of the harmogram, would lack substance without the field work of my colleague T. Maciá. Since the summer of 1993, when I gave him the first computer version of the tools that we are using, he has been testing these ideas and contributing to the symbolic appraisal of numbers that is central to all harmonic research. In the neighborhood of T. Maciá, several persons, like J. Canals and J. M. Saiz, have contributed greatly in the symbolic, interpretative and fieldwork.
Appendix One: How to Compute the Harmonic Vector.
The Harmonic Vector of a set of planetary positions {pi, i=1..n} is the Fourier spectrum of the sum of one Periodic Delta of Dirac at each planetary position pi.
To obtain it, for each natural number h (h=0,1,2..infinity), compute:
C(h) = S Cos(h x pi) and S(h) = S Sin(h x pi), sums that extend over the n values in the set of positions. Then obtain the amplitude and phase of the h-th harmonic by:
A(h) = Sqrt(Sqr(C(h)) + Sqr(S(h)))
W(h) = ArcTan(S(h)/C(h))
Geometrically speaking each pair [A(h),W(h)] is the pair of polar coordinates of the vector sum of one vector (of length 1 and angle h x pi) for each planetary position in the set. For h=1 we get the Planetary Resultant of A. Boudineau. As a matter of fact, for every h, the h-th coordinate of the Harmonic Vector of a radix is the Planetary Resultant of the h-harmonic chart.
Appendix Two: The Cyclic Index as Harmogram
A Kollerstrom & O'Neill harmogram for harmonic one computes the intensity of a conjunction as the maximum allowed orb minus the true instantaneous orb. The cyclic index of Gouchon and Barbault (Barbault 1979, see also Baigent, etc. 1984) is computed adding all the angular distances of pairs formed with the outer planets plus Saturn and Jupiter.
It should be obvious that if we allow an orb for the conjunction of 180 degrees, a harmonic-one harmogram -including from Jupiter to Pluto- gives the reversed shape of the cyclic index. See figure 10. The point stated in the Introduction concerning this matter is proved.
Figure 10.- Cyclic Index of Gouchon and Barbault vs. equivalent harmogram

In the text I've proposed, in order to have an insight into the 'harmonic energies' involved, to compute the Fourier spectrum of the intensity function used in a harmogram. Let's do so:
The spectrum of a triangular shaped wave that rises linearly from zero at a distance of 180 degrees and gets to a peak value of 1 at the partile conjunction -to 1, as I'm using normalized functions- is depicted in figure 11. In view of figure 11, to omit all harmonics but the first, seems to me the more natural simplification to that spectrum. As there is always convenient to have a constant term added to avoid negative values in the harmogram, let's say that my intensity function is:
Figure 11.- Spectrum of a harmogram function for the Cyclic Index

F0 + F1 x Cos(w), where w is the angular distance whose intensity I want to compute. As I use normalized non negative functions, it is convenient to make both coefficients equal and divide by its sum to get a peak value of 1 at the partile conjunction. That gives {F0 = 0.5 and F1 = 0.5}.
Having computed the harmonic vector {[A(0),W(0)], [A(1),W(1)], ...} of the set of the positions of Jupiter to Pluto at each moment in time -and we need only the 0-th and the first components, as all other weights in the intensity function are zero-, we get a harmonic one dynamic as is shown, in figure 12, along with the harmogram trace depicted in figure 10. The concordance is so good, as the suppressed harmonics are of low coefficient, that I've had to shift one of the traces in figure 12. The final formula for this simplified harmogram is:
n2/2 + (A(1))2/2, as a function of time
Figure 12.- Simplified spectrum (without subharmonics) harmogram of Jupiter through Pluto, compared to the harmogram trace in figure 10.

So the cyclic index has the reversed behavior of (I don't mean an exact correspondence, to the decimal figures, with) the square of coordinate one of the harmonic vector of the set of planetary positions of Jupiter to Pluto: Boudineau's Planetary Resultant [squared] for these planets. Should Boudineau have draw the evolution of the value of his Planetary Resultant as a function of time, and see its implications, he would probably had been lead, half a century earlier, to the discovery of my ideas here presented, about harmonics and harmograms. If he did, I know of no record, though he says that his device could be of use in Mundane Astrology.
I've wrought this example to the fore because of its historical interest (that I hope that it has), and because it is the first example of a special kind of harmogram that I call single harmonic harmograms. In these, I omit the constant factor and do not take the square of the amplitude. I'm not going to develop further the idea in this paper, but I know since my early work with the harmonic vector in 1990 and 1991 that they have some intrinsic potential, as a special tool, outside of what I've exposed here (see García, 1991).
As we are speaking about Barbault and the Cyclic Index, I present figure 13, as a final thought provoker.
Figure 13.- 1-2-3 Single harmonic harmogram covering Second World War time span

V1 can be read as autonomous behavior/volition exertion.
V2 as identification of enemies/formation of parts.
And V3 as development/expansion/movement/easy flow.
References
Addey, John (1972). Astrology Reborn.
Addey, John (1976). Harmonics in Astrology. Fowler.
Apostol, Tom M. Mathematical Analysis. Addison-Wesley, 2nd edition.
Baigent M., Campion N. and Harvey C. (1984). Mundane Astrology. Aquarian.
Barbault Andre (1979). Astrología Mundial. (Spanish edition).
Boudineau, Andre (1985). Bases Scientifiques de l'Astrologie. Editions Traditionnelles.
Brahy, L. G. (1934). La Clef de la prevision des événements mondiaux et des fluctuations économiques et boursières. Editions Traditionnelles. Cuarta edición de 1989.
Carslaw, H. S. (1930). An Introduction to the Theory of Fourier's Series and Integrals. Dover edition of 1950.
Dean, Geoffrey. (1996). Key Topic 3 - Theories of Astrology. Correlation 15-1, p35.
García, Miguel (1991). El Análisis Armónico como Modelo de Técnicas Astrológicas (The Harmonic Analysis as a Model for Astrological Techniques). Presented at the VIII Iberian Astrology Congress at Málaga. Privately published by the author.
García, M. (1994) Naturaleza Holográfica de la Impronta Natal (Holographic Nature of the Natal Imprint). Proceedings of the First Encounter of Astrologers at Madrid.
Hamblin, David (1983). Harmonic Charts. Aquarian.
Hawley, Kevin (1995). The Determination of Expected Harmonic Aspect Frequencies. Correlation 14-1, p38.
Kollerstrom, N. & O'Neill, M. (1991). The Harmogram. Privately published by the authors.
Kollerstrom, N. & O'Neill, M. (1996). The Eureka Effect. Urania Trust.
Maciá, T. & García, M. (Valencia, 1994). Figuras de Aspectos: Teoría y Práctica (Aspect Patterns: Theory and Practice). Proceedings of the XI Iberian Astrology Congress at Valencia.
Maciá, T. & García, M. (Peñíscola 1994). Tránsitos Armónicos (Harmonic Transits). Proceedings of the VI Astrological Meeting at Peñíscola.
Maciá, T. & García, M. (Barcelona, 1997). Armónicos: Teoría y Práctica (Harmonics: Theory and Practice). Presented at the International Astrology Congress at Barcelona. The Theory part privately published by the author.
Rudin, Walter (1987). Real and Complex Analysis. 3rd edition. McGraw-Hill.
Santos, Demetrio (1976). Investigaciones sobre Astrología. Editora Nacional.
Santos, D (1994). Principios Astrológicos y Casas Fotoeclípticas (Astrological Principles and Photoecliptic Houses). Proceedings of the VI Astrological Meeting at Peñíscola.
Zemanian, A. H. (1965). Distribution Theory and Transform Analysis. Dover edition of 1987.
|
http://cura.free.fr/xxv/25garcian.html ----------------------- All rights reserved © 2003 Miguel García Ferrández |
|
|
 |
|