A new angle on the Gauquelin Effect
by Graham Douglas
Introduction In a series of recent papers in the journal Correlation (vols 25.1, 25.2 and 26.1), I have tried to explore the possibilities for understanding the Gauquelin Effect in terms of geomagnetic theory, and one of my conclusions was that there may be interesting pre-natal effects operating, especially at geocentric conjunctions and oppositions of the sun with Gauquelin planets, (= heliocentric oppositions and conjunctions respectively). This has a geophysical correlation with previous studies that have shown that these aspects are associated with solar activity outbursts, (Vassileyeva et al 1974, Wood 1972, Grandpierre 1996, Hung 2007, Seymour 1992).
It is also interesting that pre-natal lunations were considered by classical astrologers to give information on planetary strength at birth for any planet that was linked to the sun or moon at the lunation. Further, the ancient rule that planets which were placed oriental to the sun (i.e. clockwise from the sun in the birthchart) are strengthened might imply that an influence established at a prenatal conjunction or opposition was carried forward to a subsequent birth.
I also looked at a small sample of eminent people from Michel Gauquelin's book The Spheres of Destiny, who had an uncharacteristic planet in a key sector, such as SA for a famous actor, and noticed that at the moment of the pre-natal SOJU conjunction or opposition the characteristic planet was very often found in a key sector.
Here I will present a brief report of work in progress in which the moment of the most recent prenatal conjunction or opposition of the sun with Jupiter is examined for two samples of nobel prizewinners in Physics and Chemistry. These aspects occur at the same moment wherever they are viewed from on earth, but their placing in the circle of houses/Gauquelin sectors varies strongly with local time. In each case the charts for these events were constructed for the place at which birth subsequently occurred.
Despite the fact that these aspects form and separate over periods of hours or days a remarkable pattern was revealed in which the Gauquelin key planet Saturn was found in four sectors close to the axes of the AS/DS and MC/IC more frequently than expected with a high level of statistical significance.
The 4 peaks differ from the typical Gauquelin pattern in two respects however: They are of approximately equal amplitude, and they are rotated slightly anti-clockwise, so that they coincide more closely with the two axes.
Results
In Fig. 1 the time of the most recent conjunction or opposition of SO-JU has been calculated prior to each birth at the same location. SO-JU was chosen as the first aspect to study because JU is believed to have one of the strongest effects on solar activity, along with Earth and Venus, but there will always be one of these SOJU events in a 9 month period before birth whereas this may not always occur for Venus. In each of the following graphs the ascendant is at the top, corresponding to the boundary between sectors 18 and 1, while the MC lies between the boundaries of 4 and 5.
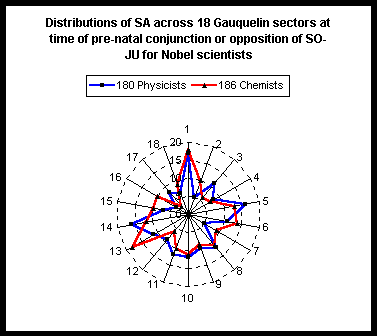
Fig.1. The distribution of Saturn in 18 sectors for two complete lists of
Nobel prizewinners 1901-2008. Dates of birth taken from Wikipedia.
Charts for most recent SO-JU aspects as they appear for the places of birth.

Fig.2. Showing the distribution for JU
In Figs 1 and 2 it can be seen that the SA distribution is similar to the typical Gauquelin pattern for scientists at birth, with a rotation of about 1 sector anticlockwise, while the JU distributions are out of step with those of SA, also as found by the Gauquelins.
To better appreciate this, Fig.3 shows the difference in frequencies SA-JU for the total of 366 scientists. In this case the mean number of births per sector is 20.33, so the amplitude of variation of the difference is striking, and the 4 –fold pattern very clear.
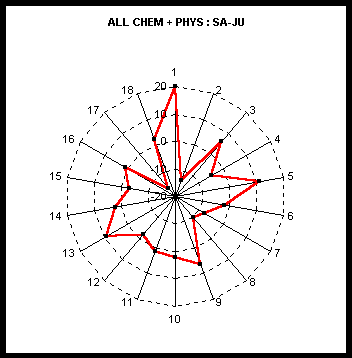
Fig. 3 Showing the difference of SA-JU frequencies for the total set of 366 scientists.
Discussion
It is important to consider how these results can be evaluated and what kinds of artifacts they might be subject to.
One thing to establish is the kind of variation to be expected when a sequence of SOJU aspect times are considered, so to do this a period of 100 years from 1862 to 1961 was selected as covering most of the period of births of these scientists, and the times of these events were calculated for one European location (London), resulting in 186 datapoints. The result is displayed in Fig.4, where it can be seen that the pattern is different, but still shows a degree of 4-fold symmetry.

Fig. 4 Showing the distribution of SA at the times of 186 SOJU events 1862-1961.
In comparing the results for scientists with this control it is important to note that the nobel winners were not all born in Europe: out of 366 a total of 164 were born in the Americas and Asia. This is especially important because the moment of conjunction or opposition is practically simultaneous all over the earth, but local time varies very significantly. It is therefore important to divide the data into 2 groups by range of latitude and examine them again.
This is done in Fig.5 and it can be seen that the same major axes of symmetry are broadly retained.
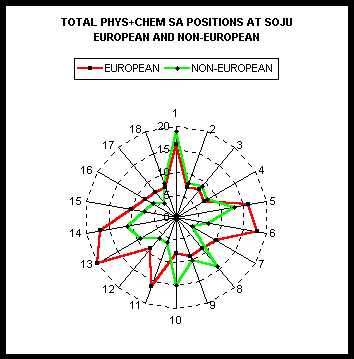
Fig.5 Showing the total distributions for 366 scientists but split
into European and non-European births.The work is at an early stage, and it is important to be cautious, especially because of the possibility of artifacts generated by resonances between planetary cycles when a set of conjunction events is selected.
If these data were birth distributions it would be sufficient to use Chi-Squared as a test of significance, and when this is done for the SA results for all 366 births the result seems impressive. Thus the Chi-Squared value (Df = 17) for the total distribution, assuming an equal expectation of SA occurrences per sector is 37.3 corresponding to a probability of chance occurrence of about 0.003; and if the data is divided into just 2 sets (those with SA in sectors 1,5,10, and 14, and the rest), then the value with Df=1 is 17.94, giving p<0.0001. For comparison the value with Df=17 for the control set (N=186) is only 14.1.
In Fig.6 the distribution of SA is shown for 202 European births only, after subtracting the scaled control distribution of Fig. 4. The major peaks at the AS and MC remain clearly visible and are now more prominent than those at the IC and DS, as is the case in a typical Gauquelin pattern.
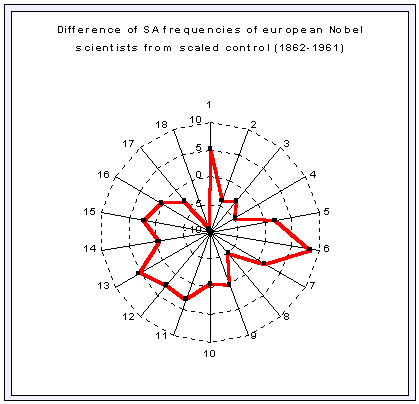
Fig.6 Showing the difference between the total European Nobel
scientists (N=202) and the scaled control distribution from Fig.4.I will now just present one further graph as a control, (Fig.7) for all Nobel prizewinners in Literature (N= 105), where again the SA pattern is different from that of scientists, but there was no pattern resembling the Gauquelin birth distributions for either venus or the moon as might have been expected.
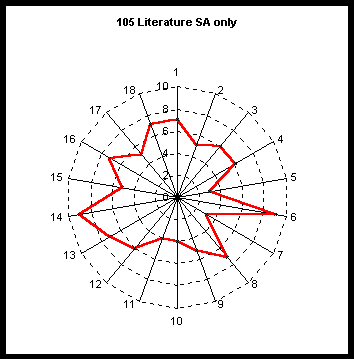
Fig.7 Showing the SA distribution for all 105 Nobel prizewinners for literature.
So, the investigation continues and I will be interested in suggestions from readers (contact G D). However one point needs to be made: even if it turns out that these patterns are the result of some combination of planetary cycle resonances this does not mean that the Gauquelin Effect is such an artifact. There is no reason to expect a series of birth times of a certain group of eminent professionals to correlate in any way with these astronomical events, unless something happens ,(such as a solar activity event) which imprints a time signature on the developing foetus which becomes a timer for its birth.
References
Blizard, Jane (1987). Long Range Predictions of Solar Activity. In: Rampino,M.R.;Sanders J.E.;Newman W.S.and Konigsson L.K. Climate: Histo ry, Periodicity and Predicatability: 415-420. New York: Van Nostrand.
Gauquelin, Michel (1980). The Spheres of Destiny. London : J.M.Dent.
Grandpierre, Attila (1996a). On the Origin of Solar Cycle Periodicity. Astrophysics and Space Science 243: 393-400.
Grandpierre, Attila (1996b). Astronomy and Astrophysics, 308:119.
Greenbaum, Dorian (2001). Late Classical Astrology: Paulus Alexandrinus and Olympiodorus with the Scholia from Later Commentators. ARHAT Publications.
Hung, Ching-Cheh (2007). Apparent Relations between Solar Activity and Solar Tides Caused by Planets. NASA Report NASA TM-2007-214817. This can be downloaded free of charge from: http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20070025111_2007025207.pdf. There are two articles with the same author and title, only this one is available for download, and it is the more comprehensive of the two.
Ibn Ezra, Abraham. The Book of Stellar Judgements.
Seymour, Percy (1988). Astrology: The Evidence of Science.
Seymour, Percy (1998). The Magus of Magnetism: An interview with Dr. Percy Seymour by Bronwyn Elko. Available on the website http://cura.free.fr, first published in The Mountain Astrologer vol.80, Aug./Sept 1988.
Vassilyeva G.I; Schpitalnaya A.A; and Petrova N.S. (1980). On the Prediction of Solar Activity taking into account its Extraneous Conditionality. In : R.F.Donnelly (ed). Solar and Terrestrial Predictions, Proceedings vol.3: A45 – A57. Washington: US Govt. Printing Office.
Wood, K.D. (1972). Sunspots and Planets. Nature, 240: 91-93.
